​一次函数k越大倾斜程度越大（一次函数k值越大图像越陡）

一次函数k越大倾斜程度越大（一次函数k值越大图像越陡）

（一）函数

1、变量：在一个变化过程中可以取不同数值的量。

 常量：在一个变化过程中只能取同一数值的量。

2、函数：一般的，在一个变化过程中，如果有两个变量x和y，并且对于x的每一个确定的值，y都有唯一确定的值与其对应，那么我们就把x称为自变量，把y称为因变量，y是x的函数。

*判断Y是否为X的函数，只要看X取值确定的时候，Y是否有唯一确定的值与之对应

3、定义域：一般的，一个函数的自变量允许取值的范围，叫做这个函数的定义域。

4、确定函数定义域的方法：

（1）关系式为整式时，函数定义域为全体实数；

（2）关系式含有分式时，分式的分母不等于零；

（3）关系式含有二次根式时，被开放方数大于等于零；

（4）关系式中含有指数为零的式子时，底数不等于零；

（5）实际问题中，函数定义域还要和实际情况相符合，使之有意义。

5、函数的解析式：用含有表示自变量的字母的代数式表示因变量的式子叫做函数的解析式

6、函数的图像

一般来说，对于一个函数，如果把自变量与函数的每对对应值分别作为点的横、纵坐标，那么坐标平面内由这些点组成的图形，就是这个函数的图象．

7、描点法画函数图形的一般步骤

第一步：列表（表中给出一些自变量的值及其对应的函数值）；

第二步：描点（在直角坐标系中，以自变量的值为横坐标，相应的函数值为纵坐标，描出表格中数值对应的各点）；

第三步：连线（按照横坐标由小到大的顺序把所描出的各点用平滑曲线连接起来）。

8、函数的表示方法

列表法：一目了然，使用起来方便，但列出的对应值是有限的，不易看出自变量与函数之间的对应规律。

解析式法：简单明了，能够准确地反映整个变化过程中自变量与函数之间的相依关系，但有些实际问题中的函数关系，不能用解析式表示。

图象法：形象直观，但只能近似地表达两个变量之间的函数关系。

（二）一次函数

1、一次函数的定义

一般地，形如（k，b是常数，且k≠0）的函数，叫做一次函数，其中x是自变量。当b=0时，一次函数y=kx，又叫做正比例函数。

⑴一次函数的解析式的形式是，要判断一个函数是否是一次函数，就是判断是否能化成以上形式．

⑵当b=0，k≠0时，y=kx仍是一次函数．

⑶当k=0，b≠0时，它不是一次函数．

⑷正比例函数是一次函数的特例，一次函数包括正比例函数．

2、正比例函数及性质

一般地，形如y=kx(k是常数，k≠0)的函数叫做正比例函数，其中k叫做比例系数.

注：

正比例函数一般形式 y=kx (k不为零)

① k不为零 ② x指数为1 ③ b取零

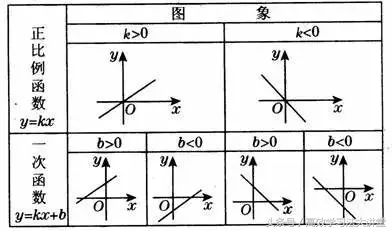
当k>0时，直线y=kx经过三、一象限，从左向右上升，即随x的增大y也增大；

当k<0时，直线y=kx经过二、四象限，从左向右下降，即随x增大y反而减小．

(1) 解析式：y=kx（k是常数，k≠0）

(2) 必过点：（0，0）、（1，k）

(3) 走向：k>0时，图像经过一、三象限；k<0时，图像经过

二、四象限

(4) 增减性：k>0，y随x的增大而增大；k<0，y随x增大而减小

(5) 倾斜度：|k|越大，越接近y轴；|k|越小，越接近x轴

3、一次函数及性质

一般地，形如y=kx＋b(k,b是常数，k≠0)，那么y叫做x的一次函数.当b=0时，y=kx＋b即y=kx，所以说正比例函数是一种特殊的一次函数.

注：一次函数一般形式 y=kx b (k不为零)

① k不为零

②x指数为1

③ b取任意实数

一次函数y=kx b的图象是经过（0，b）和（-b/k，0）两点的一条直线，我们称它为直线y=kx b,它可以看作由直线y=kx平移|b|个单位长度得到.（当b>0时，向上平移；当b<0时，向下平移）

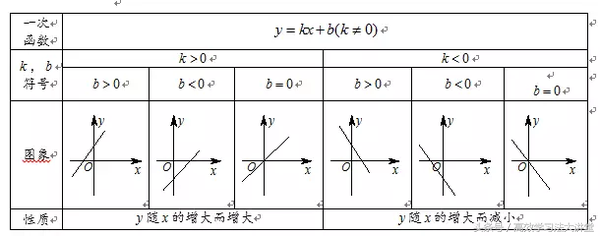
（1）解析式：y=kx b(k、b是常数，k≠0)

（2）必过点：（0，b）和（-b/k，0）

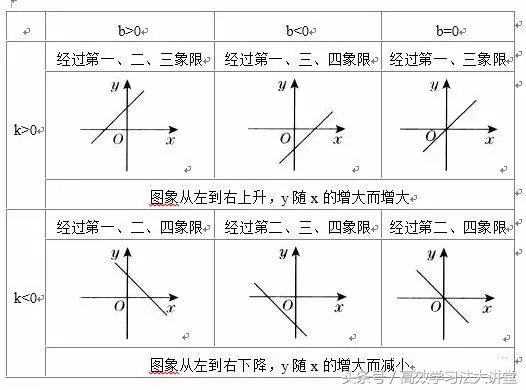
（3）走向：

k>0，图象经过第一、三象限；k<0，图象经过第二、四象限

b>0，图象经过第一、二象限；b<0，图象经过第三、四象限

直线经过第一、二、三象限

直线经过第一、三、四象限

直线经过第一、二、四象限

直线经过第二、三、四象限

（4）增减性： k>0，y随x的增大而增大；k<0，y随x增大而减小.

（5）倾斜度：|k|越大，图象越接近于y轴；|k|越小，图象越接近于x轴.

（6）图像的平移：

当b>0时，将直线y=kx的图象向上平移b个单位；

当b<0时，将直线y=kx的图象向下平移b个单位.

4、一次函数y=kx＋b的图象的画法.

根据几何知识：经过两点能画出一条直线，并且只能画出一条直线，即两点确定一条直线，所以画一次函数的图象时，只要先描出两点，再连成直线即可.一般情况下：是先选取它与两坐标轴的交点：（0，b），（-b/k，0） .即横坐标或纵坐标为0的点.

5、正比例函数与一次函数之间的关系：一次函数y=kx＋b的图象是一条直线，它可以看作是由直线y=kx平移|b|个单位长度而得到（当b>0时，向上平移；当b<0时，向下平移）

6、正比例函数和一次函数及性质

6、直线（）与（）的位置关系

（1）两直线平行且

（2）两直线相交

（3）两直线重合且

（4）两直线垂直

7、用待定系数法确定函数解析式的一般步骤：

（1）根据已知条件写出含有待定系数的函数关系式；

（2）将x、y的几对值或图象上的几个点的坐标代入上述函数关系式中得到以待定系数为未知数的方程；

（3）解方程得出未知系数的值；

（4）将求出的待定系数代回所求的函数关系式中得出所求函数的解析式.