​23个世界数学难题（最有趣最危险最复杂的世界数学难题）

23个世界数学难题（最有趣最危险最复杂的世界数学难题）

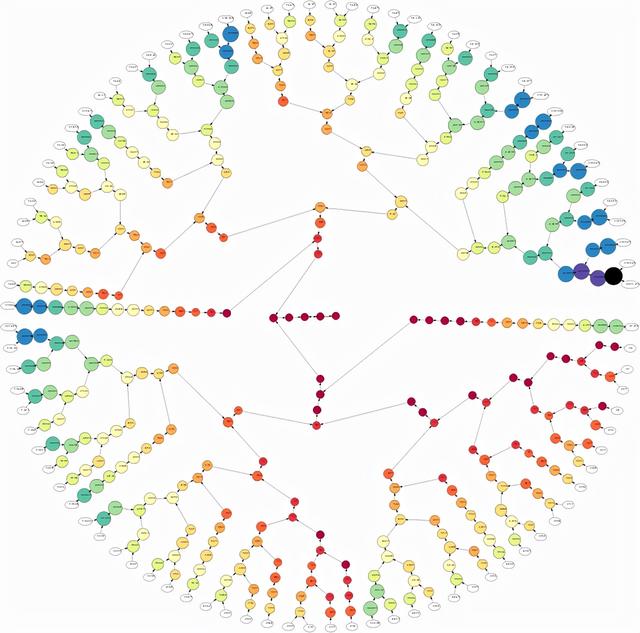
我们来玩个游戏...

任意挑选一个正整数。如果它是一个奇数，那么就乘以3再加1。如果它是一个偶数，那么就除以2。对得到的新数字做同样的事，一直这样做。如果你在某一时刻得出了数字1，那么就停止。

我知道这可能不是世界上最有趣的游戏，但请你多玩一会儿。我向你保证，这将是很有趣。

例如，如果我们从7开始，我们会得到下面的数列（从现在开始，我们称它为科拉茨序列）。

7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1.

如果我们从19开始，我们得到：

19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1.

请注意，在某一时刻，我们在上述两个序列中都得到了数字22，因此它们的“尾巴”是一样的。

问题是：我们总是在1处结束吗？

信不信由你，上述问题是一个深奥的谜题。尽管很多非常聪明的数学家做出了巨大的努力，但这个问题仍然没有得到解决。

这个问题被称为 "科拉茨猜想"。

陷入混沌

但为什么它这么难解呢？毕竟，一个孩子都会明白这个游戏的规则。它看起来非常简单。

通过对小数字的科拉茨数列的初步观察，我们没有看到什么出乎意料的情况，但当我们到了，例如，数字27，相应的序列是111步长，它在快速下降到1之前达到9232。

如果我们绘制27的科拉茨数列，我们会得到以下图表。

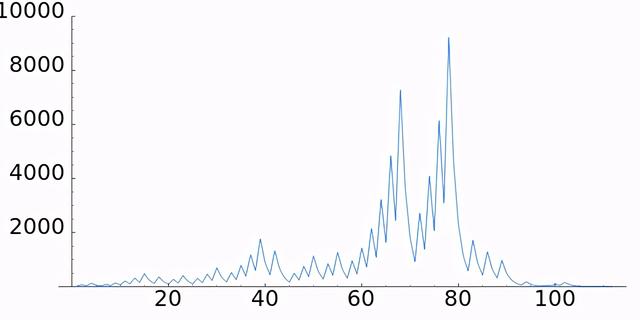
这看起来有点随机，事实上，这个问题有一定的随机性，这使得它很难处理。我们稍后会再讨论这个问题。

请注意，如果n是一个奇数，那么3n 1就是一个偶数，我们需要将其除以2，因此我们可以将这两步合并为一步，简单地说就是(3n 1)/2。

当我们把上述两个步骤结合起来时，我们会把得到的数列称为简化的科拉茨数列。

考虑一下下面的函数。

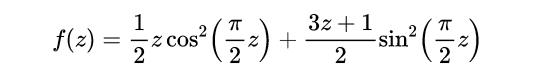
这个函数将输出简化后的科拉茨数列中的下一个数字，当然前提是z是一个整数。

但是这个函数，如果我们在复平面上定义它，是一个完整的函数，这意味着我们可以给它输入任何复数，而且它是复数可微的。

马克-张伯伦研究了这个函数在实线上的迭代，结果发现，这导致了一个动态系统。他表明，这个猜想对于所有的正实数来说并不成立，因为存在着无限多的固定点以及轨道。

下面可以看到相应的美丽的科拉茨分形。

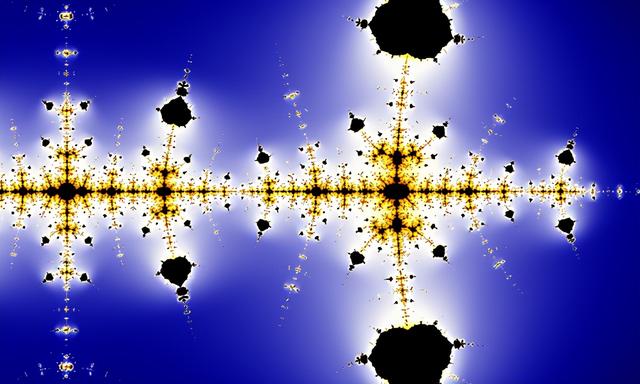
这表明，这些数列确实有一些内在的混沌性。

众所周知，动力系统和分形源于混沌系统，例如天气，其决定性特征是系统对初始条件极为敏感。

对于我们的问题来说，这意味着考虑整数和实数之间存在巨大差异，即使我们可以通过实数数列任意接近一个给定的整数，相应的科拉茨数列可能非常不同。这就造成了混乱。

解

那么，解是什么样子的呢？我们需要证明两件事。首先，我们需要证明所有数列都是有界的。换句话说，不存在无限的科拉茨数列。我所说的无限是指序列中的数字集是无限大的。第二，我们需要证明不可能出现循环。也就是说，在科拉茨数列中，我们永远不会遇到一个数字两次。如果我们从1开始，那么4，2，1的序列就会无限期地重复。

当然，还有另一种解决办法。这个猜想可能是错的，数学家试图验证它，取的起始值约为2^68。1958年，波利亚猜想（Pòlya conjecture）被一个大约1.845×10^361的反例所推翻，这比2^68这数字大得多。

实际上，这里还可能发生另一件事。数学家们往往不大谈论这个问题，因为这是很悲伤的想法。科拉茨猜想在我们的公理系统中可能是无法解决的，也就是说，无论我们如何努力，我们都无法破解它。

不要被问题的美感所迷惑

那么，为什么说这是一个危险的问题呢？

因为，当你试图解决一个数学问题，而你又不知道自己是否能够解决它时，你就把宝贵的时间都花了，最终什么也得不到。

时间是最宝贵的，而把它用在数学上是非常容易的，尤其是当一个问题看起来如此简单的时候。但事实上它一点也不简单。这就像希腊神话中的塞壬。

希腊神话中的塞壬一开始就是一群看起来像美女的生物，但实际上是吃人的野兽。他们坐在岸边，用诱人的声音唱歌，任何听到他们歌声的人都会被他们迷住。然后塞壬就会吃掉他们。

这个问题很像这样。它看起来如此美丽和简单，但在你意识到之前，你已经花费了多年的研究和精力，最终什么都没有。

实际上，许多教授警告他们的博士生不要去研究这个猜想。

真的会无功而返吗

我只是部分同意上述观点。就我个人而言，我花了很多很多时间思考黎曼假设、孪生素数猜想和科拉茨猜想，但我从不觉得自己浪费了时间，因为思考这些美丽的问题给我带来快乐。

我喜欢这个过程和挑战。即使你可能没有更接近解决实际问题，但你可能在这个过程中发展出一些公理或一些其他工具。如果不出意外，你会体会到做原始研究的感觉，并加入到许多曾经走过这条路的人中。

,