杨氏双缝干涉实验
杨氏双缝干涉实验
实验装置
1801年,英国物理学家托马斯杨首先用实验的方法观察到了光的干涉现象,这就是杨氏双缝干涉实验。该实验为光的波动学说的建立奠定了实验基础,并在历史上首次完成了光波波长的测量。
杨氏双缝干涉实验装置如图所示,
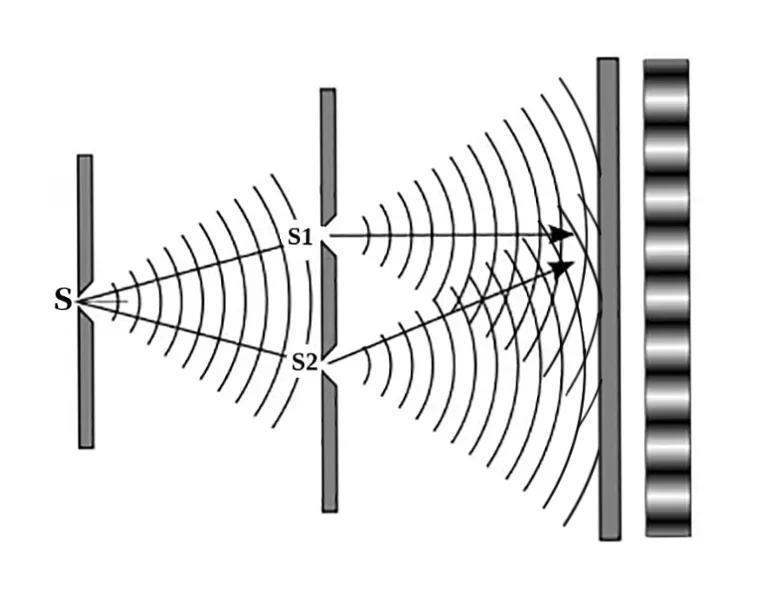
单色平行光投射到一狭缝s上,s后放置有两条与s平行,且等距的平行狭缝s1和s2。
根据惠更斯原理,s1、s2成为两个新的子波源,由于s1和s2在s发出的同一波阵面上因而具有完全相同的振动特征,构成两个相干光源。
由s1和s2发出的光波在空间相遇而产生干涉现象,在屏上形成稳定的明暗相间的干涉条纹。由于两相干光来自同一波阵面,这种获得相干光的方法称为分波阵面法。
公式推导
下面分析屏上出现明暗条纹,应满足的条件。如图所示,
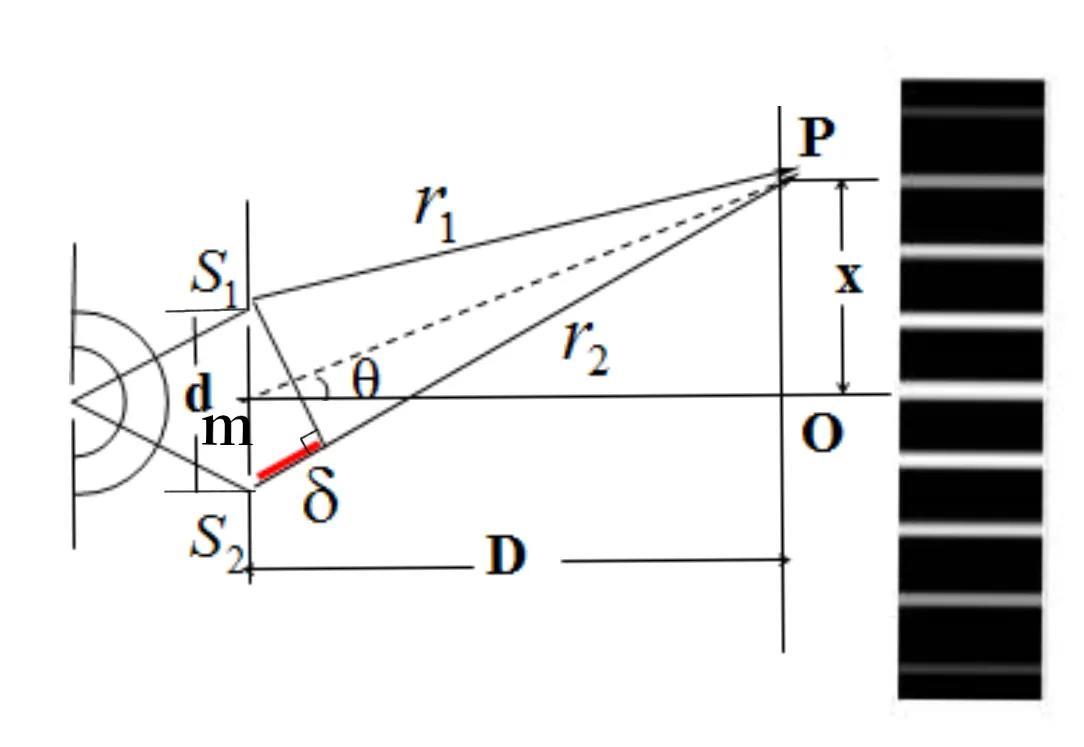
设s1、s2间的距离为d,其中点为m,从m到屏E的距离为D,且D>>d。P为屏上任意一点,P与s1和s2间的距离分别为r1和r2,P到屏的中心点o(m点在屏上的投影)的距离为x。由于θ很小,由s1s2所发出的光波到达P点的光程差δ=r2-r1近似为s1的垂足到到s2的距离,即:
δ=r2-r1≈dsinθ≈dtanθ≈dx/D
推论
若入射光的波长为λ,根据波动理论,当:
δ=dx/D=±2k·λ/2
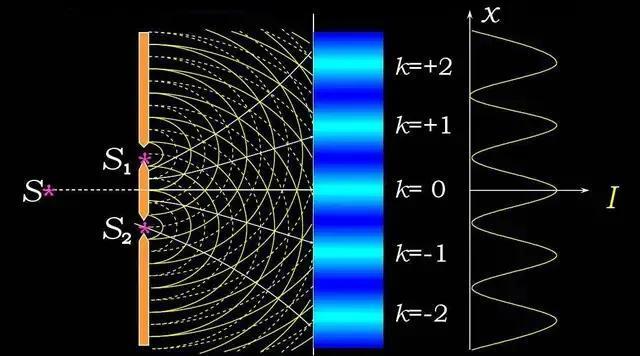
时,两光波在P点相互加强,P点处为明条纹中心。式中k为干涉级数,当k=0时,x=0,即在中心o处出现明条纹,称为中央明文或零级明纹;与k=1,2,...对应的明条纹分别称为第一级,第二级,……明纹。式中,正、负号表示条纹在中央明纹两侧对称分布。当:
δ=dx/D=±(2k-1)λ/2
时,两光波在P点相互削弱,P点处为名暗条纹中心。与k=1,2,...对应的暗条纹分称为第一级,第二级,……暗纹。
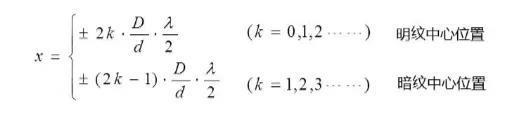
由上式相减可计算出两相邻明条纹或暗条纹中心间的距离,即条纹间距为:
△x=Dλ/d
此结果表明△x与k无关,因此,双缝干涉条纹是等间距分布的。
用不同波长的单色光源做实验时,条纹的间距不相同,波长短的单色光条纹间距小波长长的单色光条纹间距大,如果用白光做实验,只有中央铭文是白色的,其他各级都是由紫到红的彩色条纹。

-

- 何炅一家四口合照流出,父子看起来像复制粘贴,网友却抛出一个梗
-
2024-11-22 16:35:18
-
- h1z1微博正式解禁!这款被全网禁播的游戏或将被腾讯代理
-
2024-11-22 16:33:03
-

- 世界五大家族其中两个来自中国
-
2024-11-22 06:41:43
-

- 罗婕女士,是澳洲野玫瑰,是朴彩英「blackpink」
-
2024-11-22 06:39:28
-

- 李小龙到底是怎么去世的
-
2024-11-22 06:37:14
-

- 警察和公安到底有什么差别?应该怎么区分呢?可算是涨知识了
-
2024-11-22 06:34:59
-

- 火影忍者:九大尾兽的真相,九尾的实力其实一直被众人低估
-
2024-11-22 06:32:44
-

- 大门口栽什么树最好?
-
2024-11-22 06:30:29
-

- 白天看到黄鼠狼预示着什么?不只是看到黄鼠狼还看见它在捕食
-
2024-11-22 06:28:15
-

- 《地道战》(国1965)
-
2024-11-22 06:26:00
-

- 周杰伦新歌《不爱就拉倒》不爱就不爱,也请落落大方
-
2024-11-22 06:23:45
-

- 异地恋最真实的情书适合异地恋的小情话
-
2024-11-22 06:21:30
-
- 微信、QQ、TIM防撤回?一招搞定!
-
2024-11-21 21:43:19
-

- 青岛不倒我不倒,雪花不飘我不飘,不可错过31届青岛国际啤酒节
-
2024-11-21 21:41:04
-
- 盘点那些号称千年一遇的美女们
-
2024-11-21 21:38:49
-

- 韩国顶级品牌Whoo后几大系列怎么选择?看这里
-
2024-11-21 21:36:34
-

- 电视剧智能换脸怎么做到的?这个在线网站可以帮你!
-
2024-11-21 21:34:19
-

- 《还珠格格》播出24年 再看五阿哥萧剑的各自境遇 差距一目了然
-
2024-11-21 21:32:04
-

- 乡村振兴之我见
-
2024-11-21 21:29:49
-

- 盘点“向往的生活”五季蘑菇屋取景地,哪个你最向往?
-
2024-11-21 21:27:35



 泌尿外科医生提醒,不要轻易尝试“前列腺高潮”这种不安全行为
泌尿外科医生提醒,不要轻易尝试“前列腺高潮”这种不安全行为 原老民办教师10年以上补助标准
原老民办教师10年以上补助标准